Everything you need to know about Tree Traversal Algorithms: Theory and Practice in Java

In computer science, a Tree is a widely used abstract data type (ADT), or data structure implementing this ADT, that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.

A tree data structure can be defined recursively as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the “children”), with the constraints that no reference is duplicated, and none points to the root.

Thanks to Wikipedia for that great definition of Tree data structure in computer science.

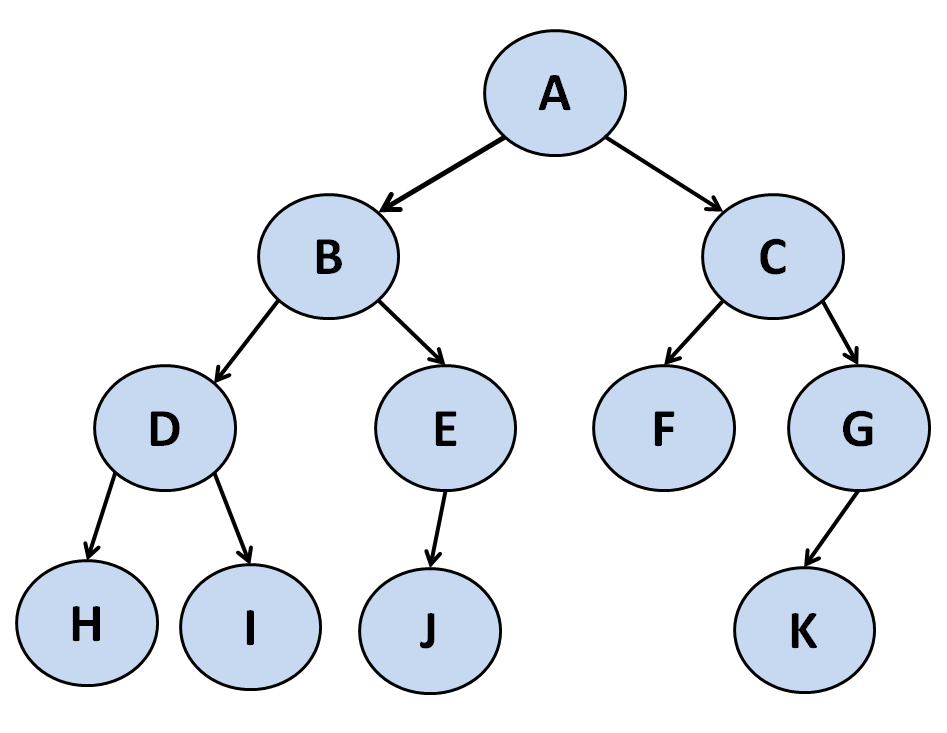
Trees can be traversed in several ways:

• Pre Order Traversal: Root, Left, Right.
  In our example: A B D H I E J C F G K
• In Order Traversal: Left, Root, Right. 
  In our example: H D I B J E A F C K G
• Post Order Traversal: Left, Right, Root. 
  In our example: H I D J E B F K G C A
• Level Order Traversal, also known as Breadth-first search. 
  In our example: A B C D E F G H I J K

In that tutorial, you are going to learn how to implement these different Tree Traversal Algorithms in Java with recursion and without recursion. Like you could see, recursion solutions are easier than iterative ones. But, you need to understand both solutions because implementing these algorithms are often asked in coding interviews.

For our examples, we will use Java programming language but the logic would be the same for implementing in other languages like C++ or Python.

Representing a Tree

First step is to represent a Tree. A Tree has nodes. So, we start by defining a Node class. A Node will have the following properties:

• data representing data of the node
• left pointer pointing to the left node
• right pointer pointing to the right node

It gives us the following Node class:

For representing a Tree, we will just have to choose a Node instance as root of the tree. It gives us the following code for the Tree building:

Tree Pre Order Traversal with Recursion

We start by implementing the Tree Pre Order Traversal Algorithm with Recursion. We want to traverse each node of the tree by displaying data for Root, Left and Right node.

So, we need to define a recursive preOrderTraverse method taking a Node in parameter and making the following operations:

• Displaying data
• Calling preOrderTraverse for the left node
• Calling preOrderTraverse for the right node

It gives us the following implementation:

You can discover the implementation and the execution of the Tree Pre Order Traversal Algorithm with Recursion in video on YouTube:

Tree Pre Order Traversal with Iterative solution

Now, things are getting a little more complicated as we will implement with a Tree Pre Order Traversal Algorithm with an Iterative solution. For that, we will need a Stack of Node.

First, we will push the Tree root in the Stack. Then, we will iterate while the Stack won’t be empty. We pop all nodes one by one and for each node, we make the following steps:

• Displaying data
• Pushing its right child in the Stack
• Pushing its left child in the Stack

It gives us the following implementation:

You can discover the implementation and the execution of the Tree Pre Order Traversal Algorithm with Iterative solution in video on YouTube:

Tree In Order Traversal with Recursion

We implement the Tree In Order Traversal Algorithm with Recursion. We want to traverse each node of the tree starting with Left node, displaying data for Root and finishing with Right node.

So, we need to define a recursive inOrderTraverse method taking a Node in parameter and making the following operations:

• Calling inOrderTraverse for the left node
• Displaying data
• Calling inOrderTraverse for the right node

It gives us the following implementation:

You can discover the implementation and the execution of the Tree In Order Traversal Algorithm with Recursion in video on YouTube:

Tree In Order Traversal with Iterative solution

Now, things are getting a little more complicated as we will implement with a Tree In Order Traversal Algorithm with an Iterative solution. We are going to use a Stack of Node. We traverse the Tree while the current node is not null or the Stack of Node is not empty.

At each iteration, we try to reach the most left node from the current node. During this nested ireration, we add each node traversed in the Stack of Node. At the end of this iteration, current node is null. So, we pop a Node from the Stack and we display its data. Finally, Now, we visit the right subtree.

It gives us the following implementation:

You can discover the implementation and the execution of the Tree In Order Traversal Algorithm with Iterative solution in video on YouTube:

Tree Post Order Traversal with Recursion

We implement the Tree Post Order Traversal Algorithm with Recursion. We want to traverse each node of the tree starting with Left node, continuing with Right Node and then displaying data for Root.

So, we need to define a recursive postOrderTraverse method taking a Node in parameter and making the following operations:

• Calling postOrderTraverse for the left node
• Calling postOrderTraverse for the right node
• Displaying data

It gives us the following implementation:

You can discover the implementation and the execution of the Tree Post Order Traversal Algorithm with Recursion in video on YouTube:

Tree Post Order Traversal with Iterative solution

Now, things are getting a little more complicated as we will implement with a Tree Post Order Traversal Algorithm with an Iterative solution. We start by creating two Stack of Node which will name nodeStack1 and nodeStack2. We push the Tree root in the nodeStack1.

We iterate while the first stack is not empty. At each iteration, we pop an item from nodeStack1 and we push it to nodeStack2. Then, we push left and right children of popped item to nodeStack1.

Then, in a second loop, we print data all the elements of nodeStack2 . This gives us the following code:

You can discover the implementation and the execution of the Tree Post Order Traversal Algorithm with Iterative solution in video on YouTube:

Tree Level Order Traversal

Finally, we are going to implement Tree Level Order Traversal Algorithm. This algorithm is also known as Breadth-First Search. We need to use an Iterative solution. The solution uses a Queue of Node. We add the Tree root.

Then, we iterate while Queue is not empty. We dequeue a node and we print the data. Then, we add children nodes if not null, left in first and right in second.

It gives us the following implementation:

You can discover the implementation and the execution of the Tree Level Order Traversal Algorithm in video on YouTube:

Conclusion

This article will have allowed you to discover the main Algorithms for Tree Traversal with their implementation in Java. The complete source of the Tree class with the main method calling all the methods presented is available just below:

To discover more tutorials, don’t hesitate to visit the SSaurel’s Channel on YouTube:

If you want to discover some books to learn Java programming, I advice you to read the following article with my selection of the Top 6 Best Books for Java programming :

Top 6 Best Books for learning Java Programming